
KNOT THEORY
Knots are all around us. We take them for granted when we tie our shoes or add a bow to a gift. But knots are much more than than appear!
Unlike your shoe laces with two ends, in the mathematical study of knots, the end of the knot strands are joined together as one continuous strand. Scientists use these knots to understand molecules and the actions of enzymes on DNA.
WHAT YOU NEED:
Sections of twine or yarn, minimum 6" long
STEPS:
-
First, watch the videos. They'll show you what you need to know to do the steps below. You might say, "What, I'm not a college student!" but we have confidence in you and, someday, when you go to college, wont it feel great to already have taken a class?! Since this can be twice as fun with a partner, you can also ask someone to do these steps with you.
-
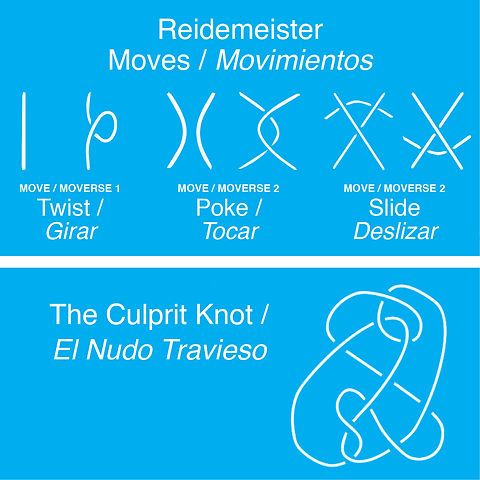
Referring to the knot diagram, try recreating the knots shown.
-
See if you can see a pattern emerging in the loops in the knots. I
Can you identify the three moves of "twist," a "poke," and a "slide"? -
Try making a random knot and then match it with a knot on the diagram. Try distinguishing knot types by using tricolorability.
-
What would knot 8 sub 1 look like?
-
Try creating a Culprit knot.
-
If you're up for a challenge, try doing a calculating knot determinant matrix as shown on the Andrews University video.
-
Finally, most challenging, trying to say "Reidemeister Moves" fives times as fast as you can while twisting, poking and sliding!

